Polygon Tutorial#
h3-py can convert between sets of cells and GeoJSON-like polygon and multipolygon shapes.
We use the abstract base class H3Shape and its concrete child classes LatLngPoly and LatLngMultiPoly
to represent these shapes.
Any references or function names that use “H3Shape” will apply to both LatLngPoly and LatLngMultiPoly objects.
h3-py is also compatible with Python objects that implement __geo_interface__ (https://gist.github.com/sgillies/2217756),
making it easy to interface with other Python geospatial libraries.
We’ll refer to any such object as a “geo” or “geo object”.
LatLngPoly and LatLngMultiPoly both implement __geo_interface__ (making them geo objects themselves),
and can be created from other geo objects, like Shapely’s Polygon or MultiPolygon objects that occur
when using geopandas.
Below, we’ll explain the h3-py API for working with these shapes, and how the library interacts
with other Python geospatial libraries.
To start, we’ll import relevant libraries, and define some plotting helper functions to visualize the shapes we’re dealing with.
import h3
import geopandas
import geodatasets
import contextily as cx
import matplotlib.pyplot as plt
def plot_df(df, column=None, ax=None):
"Plot based on the `geometry` column of a GeoPandas dataframe"
df = df.copy()
df = df.to_crs(epsg=3857) # web mercator
if ax is None:
_, ax = plt.subplots(figsize=(8,8))
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
df.plot(
ax=ax,
alpha=0.5, edgecolor='k',
column=column, categorical=True,
legend=True, legend_kwds={'loc': 'upper left'},
)
cx.add_basemap(ax, crs=df.crs, source=cx.providers.CartoDB.Positron)
def plot_shape(shape, ax=None):
df = geopandas.GeoDataFrame({'geometry': [shape]}, crs='EPSG:4326')
plot_df(df, ax=ax)
def plot_cells(cells, ax=None):
shape = h3.cells_to_h3shape(cells)
plot_shape(shape, ax=ax)
def plot_shape_and_cells(shape, res=9):
fig, axs = plt.subplots(1,2, figsize=(10,5), sharex=True, sharey=True)
plot_shape(shape, ax=axs[0])
plot_cells(h3.h3shape_to_cells(shape, res), ax=axs[1])
fig.tight_layout()
LatLngPoly#
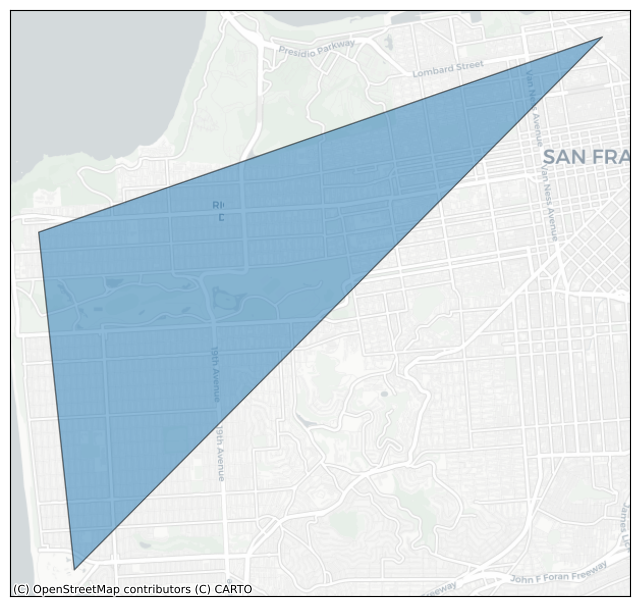
We can create a simple LatLngPoly object by providing a list of the latitude/longitude pairs that describe its exterior.
Optionally, holes can be added to the polygon by appending additional lat/lng lists do describe them.
outer = [
(37.804, -122.412),
(37.778, -122.507),
(37.733, -122.501)
]
poly = h3.LatLngPoly(outer)
print(poly)
plot_shape(poly)
<LatLngPoly: [3]>
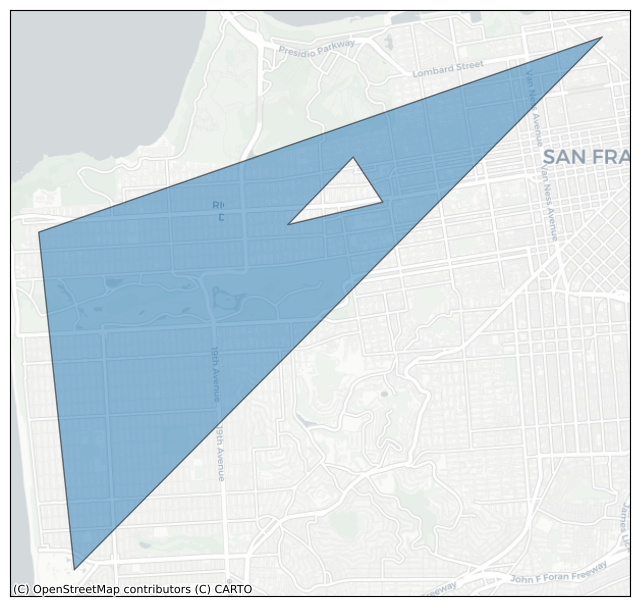
hole1 = [
(37.782, -122.449),
(37.779, -122.465),
(37.788, -122.454),
]
poly = h3.LatLngPoly(outer, hole1)
print(poly)
plot_shape(poly)
<LatLngPoly: [3/(3,)]>
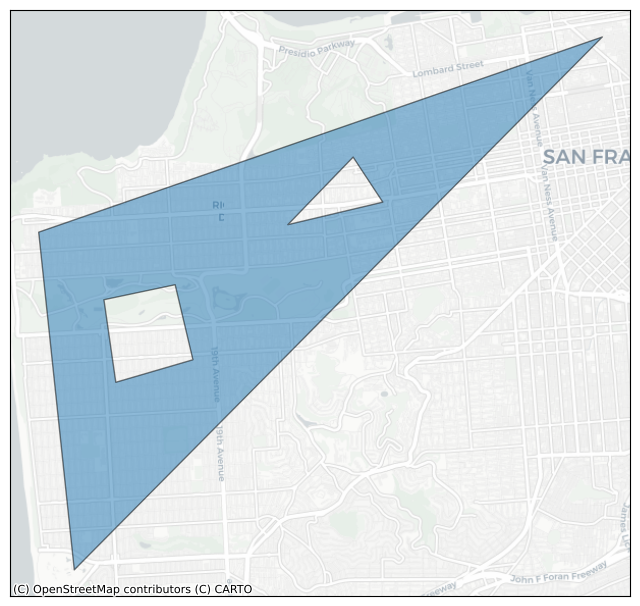
hole2 = [
(37.771, -122.484),
(37.761, -122.481),
(37.758, -122.494),
(37.769, -122.496),
]
poly = h3.LatLngPoly(outer, hole1, hole2)
print(poly)
plot_shape(poly)
<LatLngPoly: [3/(3, 4)]>
String representation and attributes#
The LatLngPoly string representation given by its __repr__ shows the number of vertices in the outer loop of the polygon, followed
by the number of vertices in each hole.
A representation like
<LatLngPoly: [3/(3, 4)]>
denotes a polygon whose outer boundary consists of 3 vertices and which has 2 holes, with 3 and 4 vertices respectively.
We can access the coordinates describing the polygon through the attributes:
LatLngPoly.outergives the list of lat/lng points making up the outer loop of the polygon.LatLngPoly.holesgives each of the lists of lat/lng points making up the holes of the polygon.
poly = h3.LatLngPoly(outer, hole1, hole2)
poly
<LatLngPoly: [3/(3, 4)]>
poly.outer
((37.804, -122.412), (37.778, -122.507), (37.733, -122.501))
poly.holes
([(37.782, -122.449), (37.779, -122.465), (37.788, -122.454)],
[(37.771, -122.484),
(37.761, -122.481),
(37.758, -122.494),
(37.769, -122.496)])
__geo_interface__#
LatLngPoly.__geo_interface__ gives a GeoJSON representation of the polygon as described in https://gist.github.com/sgillies/2217756
Note the differences in this representation: Points are given in lng/lat order (but the LatLngPoly constructor expects lat/lng order), and the last vertex repeats the first.
d = poly.__geo_interface__
d
{'type': 'Polygon',
'coordinates': (((-122.412, 37.804),
(-122.507, 37.778),
(-122.501, 37.733),
(-122.412, 37.804)),
((-122.449, 37.782),
(-122.465, 37.779),
(-122.454, 37.788),
(-122.449, 37.782)),
((-122.484, 37.771),
(-122.481, 37.761),
(-122.494, 37.758),
(-122.496, 37.769),
(-122.484, 37.771)))}
print(poly.outer)
print(poly.holes)
((37.804, -122.412), (37.778, -122.507), (37.733, -122.501))
([(37.782, -122.449), (37.779, -122.465), (37.788, -122.454)], [(37.771, -122.484), (37.761, -122.481), (37.758, -122.494), (37.769, -122.496)])
We can create an LatLngPoly object from a GeoJSON-like dictionary or an object that implements __geo_interface__ using h3.geo_to_h3shape().
h3.geo_to_h3shape(d)
<LatLngPoly: [3/(3, 4)]>
class MockGeo:
def __init__(self, d):
self.d = d
@property
def __geo_interface__(self):
return self.d
geo = MockGeo(d)
h3.geo_to_h3shape(geo)
<LatLngPoly: [3/(3, 4)]>
Also note that LatLngPoly.__geo_interface__ is equivalent to calling h3.h3shape_to_geo() on an LatLngPoly object.
poly.__geo_interface__ == h3.h3shape_to_geo(poly)
True
Polygon to cells#
We can get all the H3 cells whose centroids fall within an LatLngPoly by using h3.h3shape_to_cells() and specifying the resolution.
h3.h3shape_to_cells(poly, res=7)
['872830958ffffff', '87283095bffffff', '87283095affffff', '872830829ffffff']
We’ll use a helper function to show a few different resolutions.
plot_shape_and_cells(poly, 7)
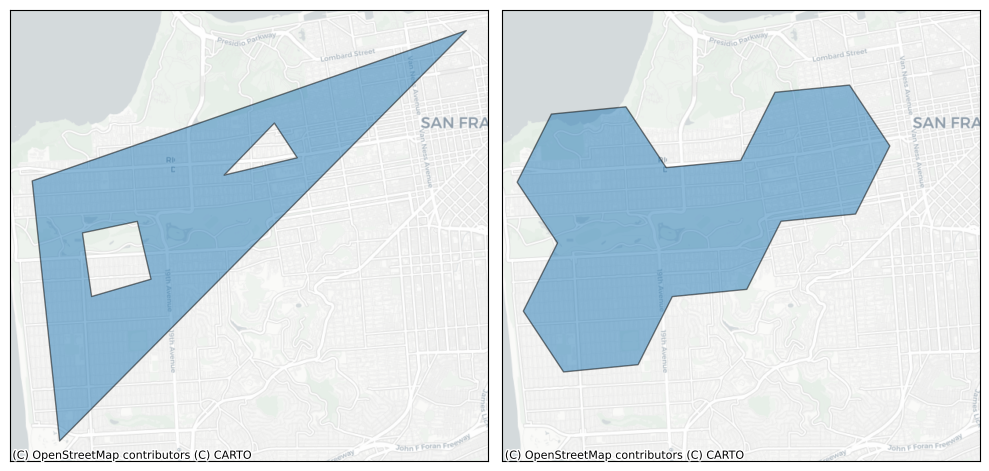
plot_shape_and_cells(poly, 9)
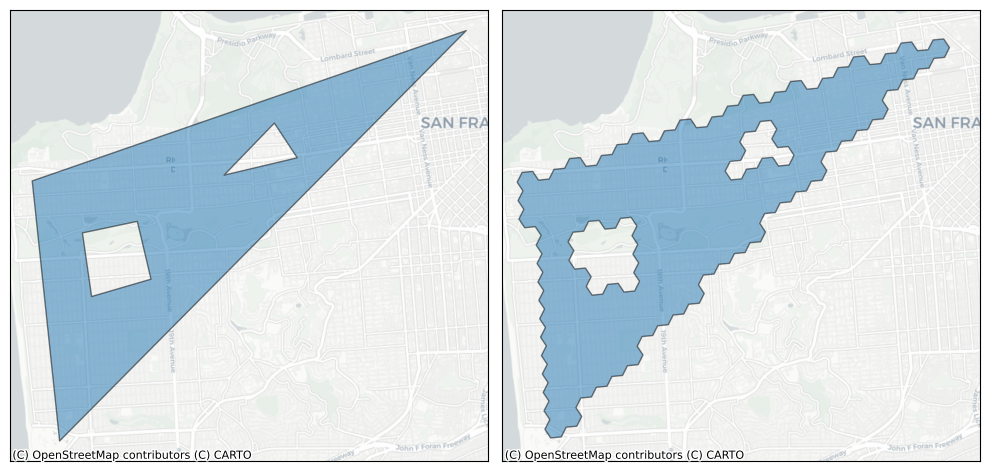
plot_shape_and_cells(poly, 10)
H3 Polygons don’t need to follow the right-hand rule#
LatLngPoly objects do not need to follow the “right-hand rule”, unlike GeoJSON Polygons.
The right-hand rule requires that vertices in outer loops are listed in counterclockwise
order and holes are listed in clockwise order.
h3-py accepts loops in any order and will usually interpret them as the user intended, for example,
converting to sets of cells. However, h3-py won’t re-order your loops to
conform to the right-hand rule, so be careful if you’re using __geo_interface__ to plot them.
Obeying the right-hand rule is only a concern when creating LatLngPoly objects from external input; LatLngPoly or LatLngMultiPoly
objects created through h3.cells_to_h3shape() will respect the right-hand rule.
For example, if we reverse the order of one of the holes in our example polygon above, the hole won’t be rendered correctly, but the conversion to cells will remain unchanged.
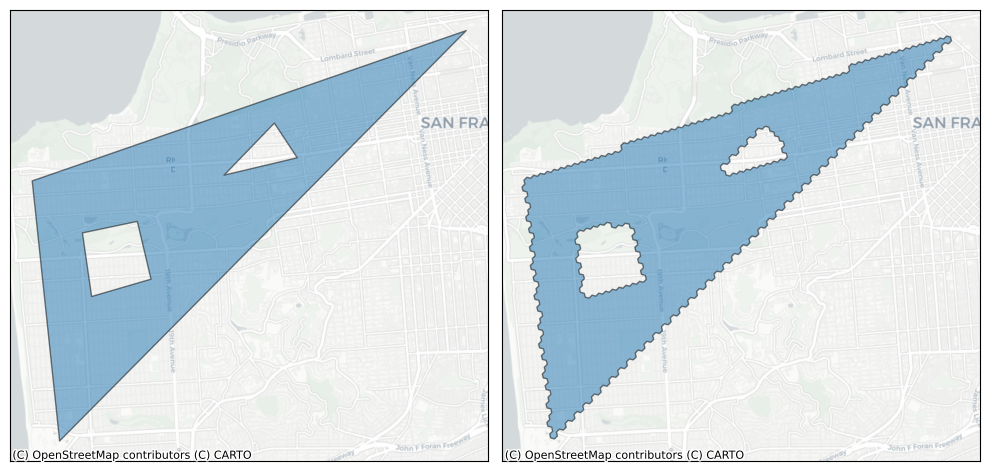
# Respects right-hand rule
poly = h3.LatLngPoly(outer, hole1, hole2)
plot_shape_and_cells(poly, res=10)
# Does not respect right-hand-rule; second hole is reversed
# Conversion to cells still works, tho!
poly = h3.LatLngPoly(outer, hole1[::-1], hole2)
plot_shape_and_cells(poly, res=10)
# Does not respect right-hand-rule; outer loop and second hole are both reversed
# Conversion to cells still works, tho!
poly = h3.LatLngPoly(outer[::-1], hole1[::-1], hole2)
plot_shape_and_cells(poly, res=10)
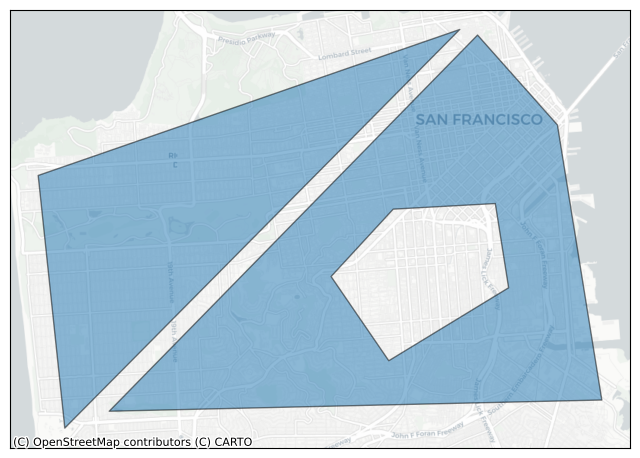
LatLngMultiPoly#
An LatLngMultiPoly can be created from LatLngPoly objects. The string representation of the LatLngMultiPoly
gives the number of vertices in the outer loop of each LatLngPoly, along with the number of vertices
in each hole (if there are any).
For example <LatLngMultiPoly: [3], [4/(5,)]> represents an LatLngMultiPoly consisting of two LatLngPoly polygons:
the first polygon has 3 outer vertices and no holes
the second polygon has 4 outer vertices and 1 hole with 5 vertices
poly1 = h3.LatLngPoly([(37.804, -122.412), (37.778, -122.507), (37.733, -122.501)])
poly2 = h3.LatLngPoly(
[(37.803, -122.408), (37.736, -122.491), (37.738, -122.380), (37.787, -122.39)],
[(37.760, -122.441), (37.772, -122.427), (37.773, -122.404), (37.758, -122.401), (37.745, -122.428)]
)
mpoly = h3.LatLngMultiPoly(poly1, poly2)
print(poly1)
print(poly2)
print(mpoly)
<LatLngPoly: [3]>
<LatLngPoly: [4/(5,)]>
<LatLngMultiPoly: [3], [4/(5,)]>
plot_shape(mpoly)
MultiPolygon to cells#
h3.h3shape_to_cells() works on both LatLngMultiPoly and LatLngPoly objects (both are subclasses of H3Shape).
cells = h3.h3shape_to_cells(mpoly, res=9)
plot_cells(cells)
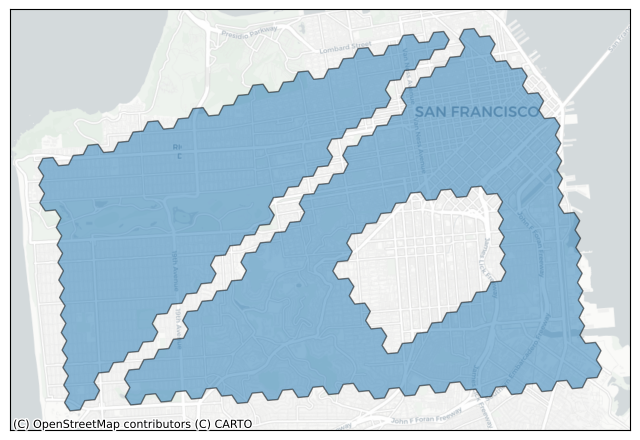
LatLngMultiPoly affordances#
Calling
len()on anLatLngMultiPolygives the number of polygonsYou can iterate through a
LatLngMultiPoly, with the elements being the underlyingLatLngPolys
len(mpoly)
2
for p in mpoly:
print(p)
<LatLngPoly: [3]>
<LatLngPoly: [4/(5,)]>
list(mpoly)
[<LatLngPoly: [3]>, <LatLngPoly: [4/(5,)]>]
__geo_interface__#
LatLngMultiPoly implements __geo_interface__, and LatLngMultiPoly objects can also be created through h3.geo_to_h3shape().
d = mpoly.__geo_interface__
d
{'type': 'MultiPolygon',
'coordinates': ((((-122.412, 37.804),
(-122.507, 37.778),
(-122.501, 37.733),
(-122.412, 37.804)),),
(((-122.408, 37.803),
(-122.491, 37.736),
(-122.38, 37.738),
(-122.39, 37.787),
(-122.408, 37.803)),
((-122.441, 37.76),
(-122.427, 37.772),
(-122.404, 37.773),
(-122.401, 37.758),
(-122.428, 37.745),
(-122.441, 37.76))))}
geo = MockGeo(d)
h3.geo_to_h3shape(geo)
<LatLngMultiPoly: [3], [4/(5,)]>
Cells to LatLngPoly or LatLngMultiPoly#
If you have a set of H3 cells that you would like to visualize, you may want to convert them to LatLngPoly or LatLngMultiPoly objects using h3.cells_to_h3shape() and then use __geo_interface__ to get their GeoJSON representation. Or you could
use h3.cells_to_geo() to get the GeoJSON dictionary directly.
h = h3.latlng_to_cell(37.804, -122.412, res=9)
cells = h3.grid_ring(h, 2)
cells
['89283082b57ffff',
'89283082b43ffff',
'89283082b4bffff',
'89283080cb3ffff',
'89283080ca3ffff',
'89283080ca7ffff',
'89283080dd3ffff',
'89283082b6fffff',
'89283082b67ffff',
'89283082b77ffff',
'89283082b0fffff',
'89283082b0bffff']
plot_cells(cells)
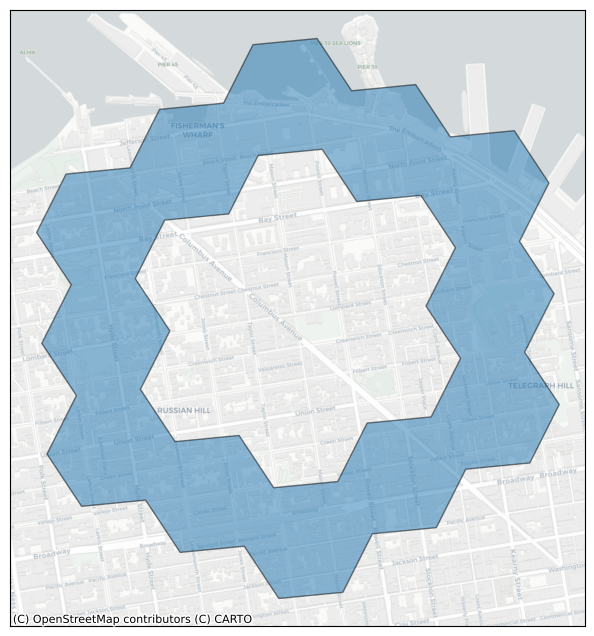
h3.cells_to_h3shape(cells)
<LatLngPoly: [30/(18,)]>
str(h3.cells_to_geo(cells))[:200]
"{'type': 'Polygon', 'coordinates': (((-122.40793197004145, 37.79671486372511), (-122.40686017324762, 37.79839728727325), (-122.40452852636689, 37.79857529774559), (-122.40345663168632, 37.800257690919"
API Summary#
"Geo object" <-> H3Shape <-> H3 cells
“Geo objects” are any Python object that implements __geo_interface__. This is a widely used
standard in geospatial Python and is used by libraries like geopandas and Shapely.
H3Shape is an abstract class implemented by LatLngPoly and LatLngMultiPoly, each of which
implement __geo_interface__ and can be created from external “Geo objects”:
geo_to_h3shape()h3shape_to_geo()
H3Shape objects can be converted to and from sets of H3 cells:
h3shape_to_cells()cells_to_h3shape()
For convience, we provide functions that hide the intermediate H3Shape representation:
geo_to_cells()cells_to_geo()
Equivalance notes#
Note that if an object a is an H3Shape
then the following two expressions are equivalent:
h3shape_to_geo(a)a.__geo_interface__
Also note that if a is an H3Shape, then a “passes through” geo_to_h3shape():
geo_to_h3shape(a) == a
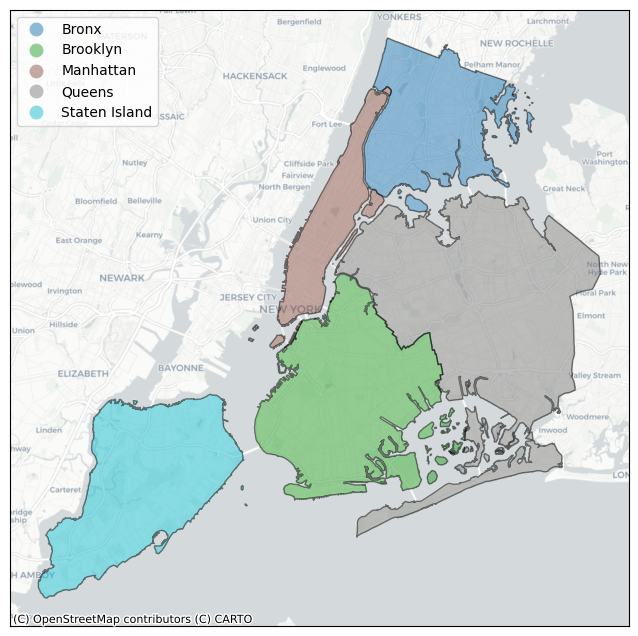
Interfacing with GeoPandas and other libraries#
The __geo_interface__ compatibility allows h3-py to work with geopandas and other geospatial libraries easily.
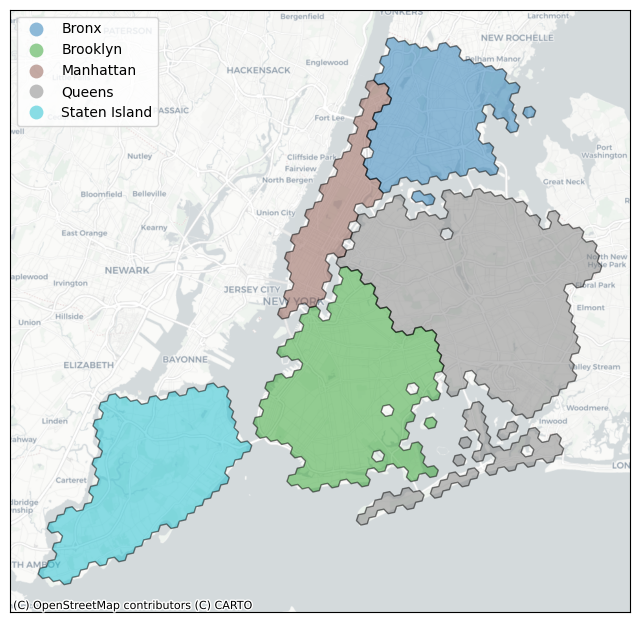
To demonstrate, we start with a GeoPandas GeoDataFrame describing the five New York City boroughs.
df = geopandas.read_file(geodatasets.get_path('nybb'))
df
Downloading file 'nybb_16a.zip' from 'https://www.nyc.gov/assets/planning/download/zip/data-maps/open-data/nybb_16a.zip' to '/home/runner/.cache/geodatasets'.
Extracting 'nybb_16a/nybb.shp' from '/home/runner/.cache/geodatasets/nybb_16a.zip' to '/home/runner/.cache/geodatasets/nybb_16a.zip.unzip'
Extracting 'nybb_16a/nybb.shx' from '/home/runner/.cache/geodatasets/nybb_16a.zip' to '/home/runner/.cache/geodatasets/nybb_16a.zip.unzip'
Extracting 'nybb_16a/nybb.dbf' from '/home/runner/.cache/geodatasets/nybb_16a.zip' to '/home/runner/.cache/geodatasets/nybb_16a.zip.unzip'
Extracting 'nybb_16a/nybb.prj' from '/home/runner/.cache/geodatasets/nybb_16a.zip' to '/home/runner/.cache/geodatasets/nybb_16a.zip.unzip'
| BoroCode | BoroName | Shape_Leng | Shape_Area | geometry | |
|---|---|---|---|---|---|
| 0 | 5 | Staten Island | 330470.010332 | 1.623820e+09 | MULTIPOLYGON (((970217.022 145643.332, 970227.... |
| 1 | 4 | Queens | 896344.047763 | 3.045213e+09 | MULTIPOLYGON (((1029606.077 156073.814, 102957... |
| 2 | 3 | Brooklyn | 741080.523166 | 1.937479e+09 | MULTIPOLYGON (((1021176.479 151374.797, 102100... |
| 3 | 1 | Manhattan | 359299.096471 | 6.364715e+08 | MULTIPOLYGON (((981219.056 188655.316, 980940.... |
| 4 | 2 | Bronx | 464392.991824 | 1.186925e+09 | MULTIPOLYGON (((1012821.806 229228.265, 101278... |
plot_df(df, column='BoroName')
Use a compatible CRS before applying H3 functions#
The function h3.geo_to_cells(geo, res) takes some “geo object” that implements __geo_interface__ (https://gist.github.com/sgillies/2217756) — like a Shapely Polygon or MultiPolygon — and converts it to the set of cells whose centroids are contained in geo.
Common Pitfall: Be careful about what CRS you are using. h3-py expects coordinates as latitude-longitude pairs. The CRS of the current dataframe (EPSG:2263) gives coordinates in feet! You should first convert the data to something compatible. A common choice is EPSG:4326/WGS84. You’ll get incorrect results if you apply h3.geo_to_cells without converting.
# Original CRS
df.crs
<Projected CRS: EPSG:2263>
Name: NAD83 / New York Long Island (ftUS)
Axis Info [cartesian]:
- X[east]: Easting (US survey foot)
- Y[north]: Northing (US survey foot)
Area of Use:
- name: United States (USA) - New York - counties of Bronx; Kings; Nassau; New York; Queens; Richmond; Suffolk.
- bounds: (-74.26, 40.47, -71.8, 41.3)
Coordinate Operation:
- name: SPCS83 New York Long Island zone (US survey foot)
- method: Lambert Conic Conformal (2SP)
Datum: North American Datum 1983
- Ellipsoid: GRS 1980
- Prime Meridian: Greenwich
df.geometry[0]
# Converting to EPSG:4326/WGS84
df = df.to_crs(epsg=4326)
df.crs
<Geographic 2D CRS: EPSG:4326>
Name: WGS 84
Axis Info [ellipsoidal]:
- Lat[north]: Geodetic latitude (degree)
- Lon[east]: Geodetic longitude (degree)
Area of Use:
- name: World.
- bounds: (-180.0, -90.0, 180.0, 90.0)
Datum: World Geodetic System 1984 ensemble
- Ellipsoid: WGS 84
- Prime Meridian: Greenwich
# Note that the `geometry` column now has coordinates in degrees
df
| BoroCode | BoroName | Shape_Leng | Shape_Area | geometry | |
|---|---|---|---|---|---|
| 0 | 5 | Staten Island | 330470.010332 | 1.623820e+09 | MULTIPOLYGON (((-74.05051 40.56642, -74.05047 ... |
| 1 | 4 | Queens | 896344.047763 | 3.045213e+09 | MULTIPOLYGON (((-73.83668 40.59495, -73.83678 ... |
| 2 | 3 | Brooklyn | 741080.523166 | 1.937479e+09 | MULTIPOLYGON (((-73.86706 40.58209, -73.86769 ... |
| 3 | 1 | Manhattan | 359299.096471 | 6.364715e+08 | MULTIPOLYGON (((-74.01093 40.68449, -74.01193 ... |
| 4 | 2 | Bronx | 464392.991824 | 1.186925e+09 | MULTIPOLYGON (((-73.89681 40.79581, -73.89694 ... |
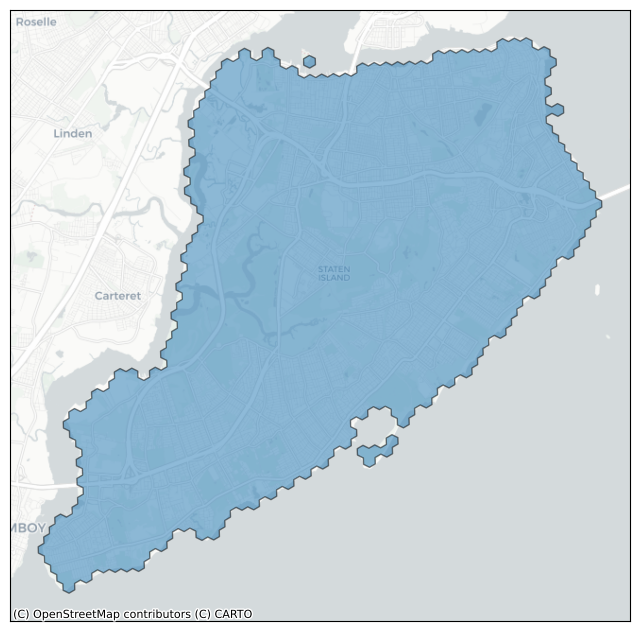
Converting a geo to H3 cells#
First, we select one of the boroughs and get the Shapely MultiPolygon describing it.
geo = df.geometry[0]
type(geo)
shapely.geometry.multipolygon.MultiPolygon
Note that Shapely MultiPolygon objects implement __geo_interface__, so we can use h3.geo_to_cells() to get the associated set of H3 cells at various resolutions.
h3.geo_to_cells(geo, res=6)
['862a1062fffffff', '862a10627ffffff', '862a1060fffffff', '862a10607ffffff']
plot_cells(h3.geo_to_cells(geo, res=9))
Converting all geos in a GeoDataFrame to cells#
We can apply geo_to_cells() to each of the Shapely geometries in the df.geometry column.
cell_column = df.geometry.apply(lambda x: h3.geo_to_cells(x, res=8))
cell_column
0 [882a106353fffff, 882a106253fffff, 882a107505f...
1 [882a103917fffff, 882a103825fffff, 882a10391df...
2 [882a1076d9fffff, 882a103929fffff, 882a107627f...
3 [882a100d0dfffff, 882a100f2dfffff, 882a100f67f...
4 [882a100f5dfffff, 882a100f43fffff, 882a100007f...
Name: geometry, dtype: object
Converting cells to “geo objects”#
If we assign df.geometry = cell_column we’ll get an error because the geometry column of a geopandas.GeoDataFrame must contain valid geometry objects.
We can obtain compatible objects by converting the cells to H3Shape by applying h3.cells_to_h3shape().
(Note that, unfortunately, Pandas has some logic to identify iterable members of a series and then renders a tuple of the elements, rather than our preferred LatLngMultiPoly.__repr__ representation.)
shape_column = cell_column.apply(h3.cells_to_h3shape)
shape_column
0 <LatLngPoly: [132]>
1 (<LatLngPoly: [178/(6,)]>, <LatLngPoly: [66/(6...
2 (<LatLngPoly: [166/(6, 6, 6)]>, <LatLngPoly: [...
3 <LatLngPoly: [120]>
4 (<LatLngPoly: [120]>, <LatLngPoly: [10]>, <Lat...
Name: geometry, dtype: object
Note that the column now consists of LatLngPoly and LatLngMultiPoly objects.
shape_column[0]
<LatLngPoly: [132]>
shape_column[1]
<LatLngMultiPoly: [178/(6,)], [66/(6,)], [22], [30], [10], [6], [6]>
Now, if we assign df.geometry = shape_column, our H3Shape objects will automatically be converted to Shapely Polygon and MultiPolygon objects via __geo_interface__.
df.geometry = shape_column
df.geometry
0 POLYGON ((-74.13326 40.54427, -74.12885 40.540...
1 MULTIPOLYGON (((-73.81285 40.64264, -73.80846 ...
2 MULTIPOLYGON (((-74.01307 40.68399, -74.01503 ...
3 POLYGON ((-74.00964 40.70522, -74.00326 40.706...
4 MULTIPOLYGON (((-73.78392 40.85395, -73.78833 ...
Name: geometry, dtype: geometry
type(df.geometry[0])
shapely.geometry.polygon.Polygon
Visualizing H3 cells#
We took some Shapely geometry objects, converted them to H3 cells, and converted those back to Shapely geometry objects in a geopandas.GeoDataFrame.
We can visualize the results with our helper function.
plot_df(df, column='BoroName')
