Backtest Orbit Model

In this section, we will cover:

• How to create a TimeSeriesSplitter

• How to create a BackTester and retrieve the backtesting results

• How to leverage the backtesting to tune the hyper-paramters for orbit models

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('ggplot')

import orbit
from orbit.models.lgt import LGTMAP, LGTAggregated
from orbit.models.dlt import DLTMAP
from orbit.diagnostics.backtest import BackTester, TimeSeriesSplitter
from orbit.utils.dataset import load_iclaims

import warnings
warnings.filterwarnings('ignore')

assert orbit.__version__ == '1.0.12'

# load log-transformed data
data = load_iclaims()

The way to gauge the performance of a time-series model is through re-training models with different historic periods and check their forecast within certain steps. This is similar to a time-based style cross-validation. More often, we called it backtest in time-series modeling.

The purpose of this notebook is to illustrate how to “backtest” a single model using BackTester

BackTester will compose a TimeSeriesSplitter within it, but TimeSeriesSplitter is useful as a standalone, in case there are other tasks to perform that requires splitting but not backtesting. TimeSeriesSplitter implemented each ‘slices’ as genertor, i.e it can be used in a for loop. You can also retrieve the composed TimeSeriesSplitter object from BackTester to utilize the additional methods in TimeSeriesSplitter

Currently, there are two schemes supported for the back-testing engine: expanding window and rolling window.

• expanding window: for each back-testing model training, the train start date is fixed, while the train end date is extended forward.

• rolling window: for each back-testing model training, the training window length is fixed but the window is moving forward.

Create a TimeSeriesSplitter

There two main way to splitting a timeseries: expanding and rolling. Expanding window has a fixed starting point, and the window length grows as we move forward in timeseries. It is useful when we want to incoporate all historical information. On the other hand, rolling window has a fixed window length, and the starting point of the window moves forward as we move forward in timeseries. Now, we will illustrate how to use TimeSeriesSplitter to split the claims timeseries.

Expanding window

# configs
min_train_len = 380 # minimal length of window length
forecast_len = 20 # length forecast window
incremental_len = 20 # step length for moving forward

ex_splitter = TimeSeriesSplitter(data, min_train_len, incremental_len, forecast_len,
                                 window_type='expanding', date_col='week')

print(ex_splitter)

------------ Fold: (1 / 3)------------
Train start index: 0 Train end index: 379
Test start index: 380 Test end index: 399
Train start date: 2010-01-03 00:00:00 Train end date: 2017-04-09 00:00:00
Test start date: 2017-04-16 00:00:00 Test end date: 2017-08-27 00:00:00

------------ Fold: (2 / 3)------------
Train start index: 0 Train end index: 399
Test start index: 400 Test end index: 419
Train start date: 2010-01-03 00:00:00 Train end date: 2017-08-27 00:00:00
Test start date: 2017-09-03 00:00:00 Test end date: 2018-01-14 00:00:00

------------ Fold: (3 / 3)------------
Train start index: 0 Train end index: 419
Test start index: 420 Test end index: 439
Train start date: 2010-01-03 00:00:00 Train end date: 2018-01-14 00:00:00
Test start date: 2018-01-21 00:00:00 Test end date: 2018-06-03 00:00:00

We can visualize the splits, green is training window and yellow it the forecasting windown. The starting point is always 0 for three splits but window length increases from 380 to 420.

_ = ex_splitter.plot()

Rolling window

# configs
min_train_len = 380 # in case of rolling window, this specify the length of window length
forecast_len = 20 # length forecast window
incremental_len = 20 # step length for moving forward

roll_splitter = TimeSeriesSplitter(data, min_train_len, incremental_len, forecast_len,
                                   window_type='rolling', date_col='week')

We can visualize the splits, green is training window and yellow it the forecasting windown. The window length is always 380, while the starting point moves forward 20 weeks each steps.

_ = roll_splitter.plot()

Specifying number of splits

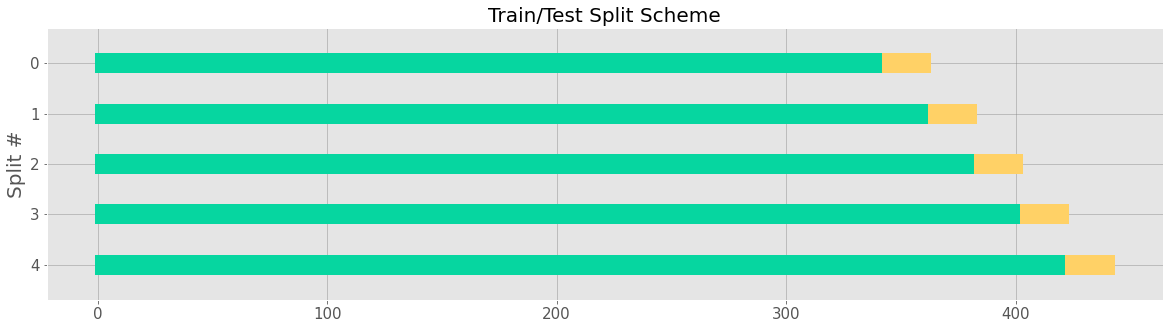
User can also define number of splits using n_splits instead of specifying minimum training length. That way, minimum training length will be automatically calculated.

ex_splitter2 = TimeSeriesSplitter(data, min_train_len, incremental_len, forecast_len,
                                  n_splits=5, window_type='expanding', date_col='week')

_ = ex_splitter2.plot()

TimeSeriesSplitter as generator

TimeSeriesSplitter is implemented as a genetor, therefore we can call split() to loop through it. It comes handy even for tasks other than backtest.

 for train_df, test_df, scheme, key in roll_splitter.split():
        print('Initial Claim slice {} rolling mean:{}'.format(key, train_df['claims'].mean()))

Initial Claim slice 0 rolling mean:12.712341458856958
Initial Claim slice 1 rolling mean:12.67144746151623
Initial Claim slice 2 rolling mean:12.64657747604057

Create a BackTester

Now, we are ready to do backtest, first let’s initialize a DLT model and a BackTester. You pass in TimeSeriesSplitter parameters to BackTester.

# instantiate a model
dlt = DLTMAP(
    date_col='week',
    response_col='claims',
    regressor_col=['trend.unemploy', 'trend.filling', 'trend.job'],
    seasonality=52,
)

# configs
min_train_len = 100
forecast_len = 20
incremental_len = 100
window_type = 'expanding'

bt = BackTester(
    model=dlt,
    df=data,
    min_train_len=min_train_len,
    incremental_len=incremental_len,
    forecast_len=forecast_len,
    window_type=window_type,
)

Backtest fit and predict

The most expensive portion of backtesting is fitting the model iteratively. Thus, we separate the api calls for fit_predict and score to avoid redundant computation for multiple metrics or scoring methods

bt.fit_predict()

Once fit_predict() is called, the fitted models and predictions can be easily retrieved from BackTester. Here the data is grouped by the date, split_key, and whether or not that observation is part of the training or test data

predicted_df = bt.get_predicted_df()
predicted_df.head()

	date	split_key	training_data	actuals	prediction
0	2010-01-03	0	True	13.386595	13.386595
1	2010-01-10	0	True	13.624218	13.640713
2	2010-01-17	0	True	13.398741	13.375456
3	2010-01-24	0	True	13.137549	13.151983
4	2010-01-31	0	True	13.196760	13.196775

Users might find this useful for any custom computations that may need to be performed on the set of predicted data. Note that the columns are renamed to generic and consistent names.

Sometimes, it might be useful to match the data back to the original dataset for ad-hoc diagnostics. This can easily be done by merging back to the orignal dataset

predicted_df.merge(data, left_on='date', right_on='week')

	date	split_key	training_data	actuals	prediction	week	claims	trend.unemploy	trend.filling	trend.job	sp500	vix
0	2010-01-03	0	True	13.386595	13.386595	2010-01-03	13.386595	0.219882	-0.318452	0.117500	-0.417633	0.122654
1	2010-01-03	1	True	13.386595	13.386595	2010-01-03	13.386595	0.219882	-0.318452	0.117500	-0.417633	0.122654
2	2010-01-03	2	True	13.386595	13.386595	2010-01-03	13.386595	0.219882	-0.318452	0.117500	-0.417633	0.122654
3	2010-01-03	3	True	13.386595	13.386595	2010-01-03	13.386595	0.219882	-0.318452	0.117500	-0.417633	0.122654
4	2010-01-10	0	True	13.624218	13.640713	2010-01-10	13.624218	0.219882	-0.194838	0.168794	-0.425480	0.110445
...	...	...	...	...	...	...	...	...	...	...	...	...
1075	2017-12-17	3	False	12.568616	12.578802	2017-12-17	12.568616	0.298663	0.248654	-0.216869	0.434042	-0.482380
1076	2017-12-24	3	False	12.691451	12.682831	2017-12-24	12.691451	0.328516	0.233616	-0.358839	0.430410	-0.373389
1077	2017-12-31	3	False	12.769532	12.732890	2017-12-31	12.769532	0.503457	0.069313	-0.092571	0.456087	-0.553539
1078	2018-01-07	3	False	12.908227	12.911066	2018-01-07	12.908227	0.527849	0.051295	0.029532	0.471673	-0.456456
1079	2018-01-14	3	False	12.777193	12.695408	2018-01-14	12.777193	0.465717	0.032946	0.006275	0.480271	-0.352770

1080 rows × 12 columns

Backtest Scoring

The main purpose of BackTester are the evaluation metrics. Some of the most widely used metrics are implemented and built into the BackTester API.

The default metric list is smape, wmape, mape, mse, mae, rmsse.

bt.score()

	metric_name	metric_values	is_training_metric
0	smape	0.006231	False
1	wmape	0.006221	False
2	mape	0.006212	False
3	mse	0.012160	False
4	mae	0.079023	False
5	rmsse	0.787080	False

It is possible to filter for only specific metrics of interest, or even implement your own callable and pass into the score() method. For example, see this function that uses last observed value as a predictor and computes the mse. Or naive_error which computes the error as the delta between predicted values and the training period mean.

Note these are not really useful error metrics, just showing some examples of callables you can use ;)

def mse_naive(test_actual):
    actual = test_actual[1:]
    predicted = test_actual[:-1]
    return np.mean(np.square(actual - predicted))

def naive_error(train_actual, test_predicted):
    train_mean = np.mean(train_actual)
    return np.mean(np.abs(test_predicted - train_mean))

bt.score(metrics=[mse_naive, naive_error])

	metric_name	metric_values	is_training_metric
0	mse_naive	0.019628	False
1	naive_error	0.226995	False

It doesn’t take additional time to refit and predict the model, since the results are stored when fit_predict() is called. Check docstrings for function criteria that is required for it to be supported with this api.

In some cases, we may want to evaluate our metrics on both train and test data. To do this you can call score again with the following indicator

bt.score(include_training_metrics=True)

	metric_name	metric_values	is_training_metric
0	smape	0.006231	False
1	wmape	0.006221	False
2	mape	0.006212	False
3	mse	0.012160	False
4	mae	0.079023	False
5	rmsse	0.787080	False
6	smape	0.002689	True
7	wmape	0.002684	True
8	mape	0.002687	True
9	mse	0.002976	True
10	mae	0.034300	True

Backtest Get Models

In cases where BackTester doesn’t cut it or for more custom use-cases, there’s an interface to export the TimeSeriesSplitter and predicted data, as shown earlier. It’s also possible to get each of the fitted models for deeper diving

fitted_models = bt.get_fitted_models()

model_1 = fitted_models[0]
model_1.get_regression_coefs()

	regressor	regressor_sign	coefficient
0	trend.unemploy	Regular	-0.049398
1	trend.filling	Regular	-0.033685
2	trend.job	Regular	0.274851

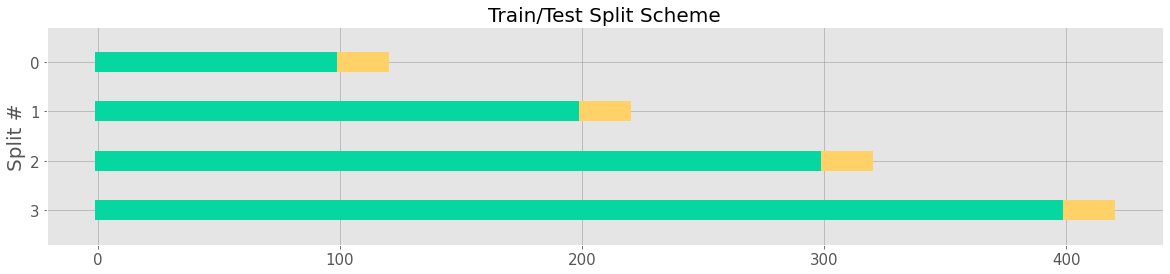
BackTester composes a TimeSeriesSplitter within it, but TimeSeriesSplitter can also be created on its own as a standalone object. See section below on TimeSeriesSplitter for more details on how to use the splitter.

All of the additional TimeSeriesSplitter args can also be passed into BackTester on instantiation

ts_splitter = bt.get_splitter()
_ = ts_splitter.plot()

Hyperparameter Tunning

After seeing the results fromt the backtest, users may wish to fine tune the hyperparmeters. Orbit also provide a grid_search_orbit utilities for parameter searching. It uses Backtester under the hood so users can compare backtest metrics for different paramters combination.

from orbit.diagnostics.backtest import grid_search_orbit
# defining the search space for level smoothing paramter and seasonality smooth paramter
param_grid = {
    'level_sm_input': [0.3, 0.5, 0.8],
    'seasonality_sm_input': [0.3, 0.5, 0.8],
}

# configs
min_train_len = 380 # in case of rolling window, this specify the length of window length
forecast_len = 20 # length forecast window
incremental_len = 20 # step length for moving forward
best_params, tuned_df = grid_search_orbit(param_grid,
                                        model=dlt,
                                        df=data,
                                        min_train_len, incremental_len, forecast_len,
                                        metrics=None, criteria=None, verbose=True)

  0%|          | 0/9 [00:00<?, ?it/s]

tuning hyper-params {'level_sm_input': 0.3, 'seasonality_sm_input': 0.3}

 11%|█         | 1/9 [00:00<00:03,  2.51it/s]

tuning metric:0.0069549
tuning hyper-params {'level_sm_input': 0.3, 'seasonality_sm_input': 0.5}

 22%|██▏       | 2/9 [00:00<00:02,  2.49it/s]

tuning metric:0.0064769
tuning hyper-params {'level_sm_input': 0.3, 'seasonality_sm_input': 0.8}

 33%|███▎      | 3/9 [00:01<00:02,  2.49it/s]

tuning metric:0.0062834
tuning hyper-params {'level_sm_input': 0.5, 'seasonality_sm_input': 0.3}

 44%|████▍     | 4/9 [00:01<00:02,  2.37it/s]

tuning metric:0.0074489
tuning hyper-params {'level_sm_input': 0.5, 'seasonality_sm_input': 0.5}

 56%|█████▌    | 5/9 [00:02<00:01,  2.39it/s]

tuning metric:0.0070464
tuning hyper-params {'level_sm_input': 0.5, 'seasonality_sm_input': 0.8}

 67%|██████▋   | 6/9 [00:02<00:01,  2.25it/s]

tuning metric:0.0066297
tuning hyper-params {'level_sm_input': 0.8, 'seasonality_sm_input': 0.3}

 78%|███████▊  | 7/9 [00:03<00:01,  1.95it/s]

tuning metric:0.0094182
tuning hyper-params {'level_sm_input': 0.8, 'seasonality_sm_input': 0.5}

 89%|████████▉ | 8/9 [00:03<00:00,  1.85it/s]

tuning metric:0.0088091
tuning hyper-params {'level_sm_input': 0.8, 'seasonality_sm_input': 0.8}

100%|██████████| 9/9 [00:04<00:00,  2.05it/s]

tuning metric:0.0078637

tuned_df.head() # backtest output for each parameter searched

	level_sm_input	seasonality_sm_input	metrics
0	0.3	0.3	0.006955
1	0.3	0.5	0.006477
2	0.3	0.8	0.006283
3	0.5	0.3	0.007449
4	0.5	0.5	0.007046

best_params # output best parameters

[{'level_sm_input': 0.3, 'seasonality_sm_input': 0.8}]